Dan writes:
>
> Hello Barrett,
>
> I'm a beginning guitarist, and I've been working my way
> through your "Guitar Fretboard Workbook". It is a great
> workbook, and I really like your style of "read it, write
> it, play it" which really helps me learn.
>
> As you state late in Chapter 22, I've been constructing a
> final project workbook with all sorts of shapes, chords,
> scales, and arpeggios. However I am confused by one item.
> You recommend to make diagrams of 72 triads (12 major, 12
> minor, etc.). I cannot figure out how to come up with 12
> major triad chords. In chapter 14 you show five patterns of
> each triad and then talk about inversions, but I still can't
> figure out how you come up with 12. Did you mean 15? Five
> triad patterns plus five first inversions plus five second
> inversions?
>
> Please let me know how to come up with a good practice list
> for triads.
>
> Thanks, Dan
>
Hi Dan,
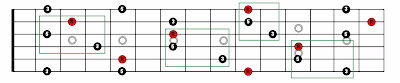
The last sentence on page 44 of Chapter 14 says, "We will divide each (triad shape) into four small three-string shapes..."
Here is another way to look at it that I think you'll find helpful.
If you stay on one stringset (a group of adjacent strings), there are three triad voicings. Play this example on the top three strings for D major.
-2--5--10-----
-3--7--10-----
-2--7--11-----
--------------
--------------
--------------
Those are, in order, 2nd inversion, root position, and 1st inversion.
On the next string set, the same D major triad goes like this:
--------------
-3--7--10-----
-2--7--11-----
-4--7--12-----
--------------
--------------
Those are 1st inversion, 2nd inversion, root position.
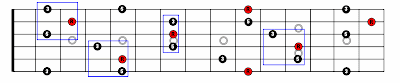
Following this systematic exhaustion we have 4 possible sets of adjacent strings: 321 432 543 654. Multiply that 4 by the 3 inversions on each stringset and you get 12 close-voiced triads.
Here are the major triads on the other two stringsets.
--------------
--------------
-2--7--11-----
-4--7--12-----
-5--9--12-----
--------------
-------------
-------------
-------------
-4--7---12---
-5--9---12---
-5--10--14---
The list does not yet include any open-voiced triads like this, which would greatly increase the number of permutations:
-5-
-3-
---
-4-
---
---
Some of the inversions are shared by two root shape/pattern numbers. For example, this voicing is shared by Pattern 2 and Pattern 3.
---
-7-
-7-
-7-
---
---
Thanks for your mail, and congratulations on finishing the book.
All the best,
Barrett